Il y a une dizaine de jours, en « feuilletant » Twitter,
je suis tombé sur cette question d’une collègue qui se désespérait de ne pas
réussir à convaincre ses élèves que oui, un carré est un
rectangle. Et qui lançait un appel à l’aide : quelqu’un aurait-il l’idée de
manipulations matérielles qui lui permettraient d’y arriver.
Et là, je ne suis pas d’accord avec ma collègue (dont par
ailleurs j’apprécie les interventions) : des manipulations, il y en a… ou plus
exactement il y en aurait plein – et
j’y reviendrai. Mais en amont de ces éventuelles manipulations il manque une
volonté, celle de construire la géométrie au collège.
Cette volonté manque cruellement dans les programmes. Bon,
j’ai déjà largement eu l’occasion de gémir là-dessus dans un article d’Images
des mathématiques – Collèges : veut-on mettre la géométrie à la poubelle ? – alors
je ne vais pas recommencer ici, mais ce laxisme officiel a malheureusement un
effet pernicieux sur les professeurs eux-mêmes : si leur hiérarchie leur fait
clairement comprendre qu’ils peuvent (doivent ?) se contenter d’appliquer
la géométrie à quelques situations bien convenues, pourquoi voulez-vous qu’ils
en fassent plus ?
Il est invraisemblable que la majorité des élèves de
collège puisse encore confondre longueur et aire (parce qu’ils confondent ligne et surface) et de nombreux
collègues s’en exaspèrent… peut-être parce qu’il s’agit d’une de ces situations
convenues commentées par leur hiérarchie.
Il est tout aussi invraisemblable qu’une majorité
d’élèves se demande encore si un carré est un rectangle, mais là, les collègues
qui s’en exaspèrent sont bien plus rares. J’ai même eu des commentaires de
personnes qui trouvaient cette question légitime, voire même qui « estimaient
» qu’un carré n’était pas un rectangle.
Et pourtant, est-ce qu’un professeur cesse d’être un être
humain ? Euh, au vu des réactions de certains élèves, la question est
peut-être mal choisie, alors :
est-ce qu’un chat noir cesse d’être un chat ? Bon, oui,
dans certains manuels de sorcellerie, mais dans la réalité ?
Toute cette polémique a pour origine l’ignorance d’un des principes de la
logique qui nous est habituelle : un objet (au sens large, êtres vivants
compris) auquel on découvre une nouvelle propriété ne cesse pas d’être ce qu’il
était avant cette découverte.
Plus « scientifiquement » : si parmi les objets d’une
catégorie A, on découvre à certains une caractéristique supplémentaire par
rapport aux autres, ces objets seront toujours des A… peut-être, s’ils sont
suffisamment intéressants ou nombreux les appellera-t-on des A+ ou des A-B.
Peut-être même s’ils sont suffisamment exceptionnels finira-t-on par les
appeler simplement des B, mais toutes les personnes instruites sauront
que ces B sont des cas particuliers de A !
« Ignorance »…
« instruites »… rappelez-moi : quel
est le but de notre système d’éducation ?
Rappelez-moi encore : quel paragraphe, quelle ligne, quel
mot des programmes officiels incite les professeurs de mathématiques à – oh non
pas construire, mais tout au moins ébaucher une arborescence de notre géométrie
? Je ne parle même pas d’en introduire les éléments dans un ordre logique
plutôt que de les jeter en vrac et en pâture à un public captif.
Bon, je ne vais pas rêver : ma voix ne portera pas bien
loin.
Mais je peux au moins proposer quelques éléments de
réponse, quelques manipulations plus ou moins matérielles à ma collègue
désespérée – ne serait-ce que parce que critiquer sans rien proposer… non,
vraiment non !
Je dois toutefois vous en avertir : ça va vous prendre du
temps ! Mais après tout, du temps j’en ai bien pris, moi, pour vous préparer
tout ça, pour le mettre en forme, alors… pourquoi pas ?
Pour commencer, je vous propose de lire les feuilles de
cours que je distribuais à mes élèves, il y a encore 5 ans :
cours-5-Parallelogrammes.pdf
(oui évidemment, vous pouvez les imprimer, elles sont à
votre disposition)
Ensuite, et ça, ça ne prendra pas longtemps du tout,
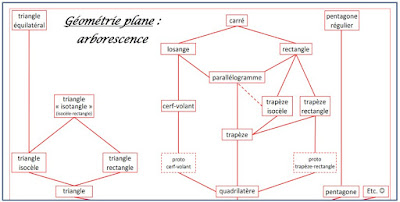
voici (également à votre disposition) l’introduction aux quadrilatères dans «…
donc, d’après… » – et surtout une arborescence qui pourrait être à l’origine de
nombreuses manipulations : par exemple en créant une version « muette » de
cette arborescence (c’est-à-dire une version dans laquelle les noms des objets
seraient remplacés par LA propriété qui les caractérise par rapport à leur
ascendant direct), en projetant cette version muette sur un tableau blanc puis
en faisant tirer à un élève une carte parmi un jeu de cartes contenant les noms
de toutes les figures planes au programme et en lui demandant de suivre le
chemin correspondant sur l’arborescence. Il – ou elle – pourrait même gagner
des points en avançant dans sa progression… ou tout perdre en voulant aller
trop loin ou en se trompant de chemin :
http://donc-dapres.com/ebauches/textes/P3-intro-arborescence.pdf
Enfin, mais là il faudrait vraiment que vous ayez une
vingtaine de minutes à perdre, vous pourriez regarder la vidéo présentée dans
le lien suivant, une version imprimée de l’arborescence à la main : vous y découvririez
(à partir de la marque 4 minutes 40) un autre type de manipulation… et une
utilisation bien peu conventionnelle d’un compas et d’une règle 😊.
(Pour la petite histoire, c’est réellement par cette
manipulation que je présentais l’arborescence des parallélogrammes à mes élèves
de cinquième !)
https://mathemagique-com.blogspot.com/2015/02/vous-avez-dit-parallelogrammes.html
Ah oui, j’allais oublier : l’accès
aux versions numériques de «… donc, d’après… » et du tome 1 du « cours de
mathématiques du cycle quatre » reste gratuit jusqu’à la fin de la pandémie… alors
n’hésitez pas :
Donc d’après Cours de mathématiques, tome 1
Merci de votre fidélité à ce blog,
Philippe Colliard